Loop mechanics-A review

Components of a loop

Loops consists of horizontal force system, vertical force system, alpha bend, beta bend and helical component. Each loop is constructed with one or more of the above components. Specific component of each loop has been mentioned under the respective loop. 2

Classification of loops

Based on configuration

Based on purpose of the loop

Based on presence of helix

Based on function

Vertical loop- Robert strang (Figure 1)

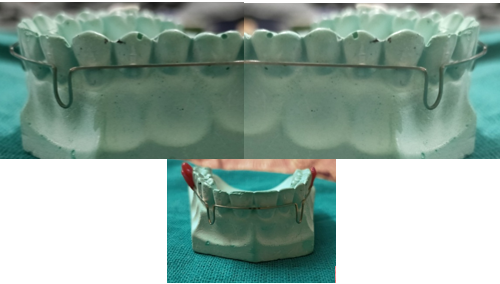
It is made out of 0.016" SS wire, and it is 6mm by height. Vertical loops can be used to open or close spaces and rotate teeth. They can also be closing loops or opening loops.1 Burstone discussed the vertical loop's force system in terms of retraction mechanics. A typical clinical application generates a force deflection rate of 437g/mm and a moment to force ratio of 2.2mm at a vertical height of 6mm. For uncontrolled tipping, a moment to force ratio of 2.2mm is insufficient. The height of the loop can be increased to increase the moment to force ratio. This height can be increased by adding a helix, although helixes with more than three turns are ineffective. As the helix is positioned more apically, the M/F ratio rises linearly, further lowering force deflection rate. In Beggs mechanotherapy, archwires with vertical loops are used to align the anterior teeth. The loops make the wire stretch wider between the teeth and result in softer pressure when the object is moved. A circular cuspid hook that lies on either side of the mesial aspect of the cuspid bracket is used to create the looped arch. In order to create overcorrection of rotations, labio-lingual movement, or mesio-distal movement, the loops are then activated.

Figure 1

Vertical Loop

Horizontal loop / Boot loop- Morris M. Stoner in 1960 (Figure 2)

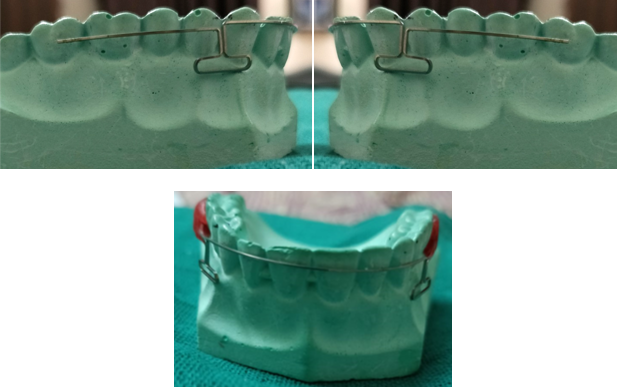
It is formed by placing the active legs parallel to the arch wire. Incorporating a horizontal loop allows greater control over the direction of the force.5 A horizontal loop provides for more precise control over the force's direction.5 The main benefit of the horizontal loop is the decrease in vertical plane or occluso-gingival force, which enables fast bracket engagement in severely positioned teeth that the operator may desire to elevate or depress.

It works well for opening bites. On extremely packed teeth, immediate bracket engagement is feasible without using excessive force. The horizontal loop can be shaped to press against the gingival area and create a torquing activity on the root, however this has not been found to be very effective in clinical trials. The double Horizontal Loop performs best when it is kept on a single tooth either above or below the line of occlusion.5

Figure 2

Horizontal/Boot Loop

Asymmetric T loop- James hilger in 1992 (Figure 4)

This loop enables bite opening and space closure at the same time. It is constructed using TMA wire that is either 0.016" X 0.022" or 0.019" X 0.025" with a 5mm vertical step, a 2mm anterior loop, a 5mm posterior loop, and an accentuated reverse Spee curve.6 Short mesial loop compression and extended distal loop opening are used to activate the asymmetric T loop.

Figure 3

Segmental T Loop

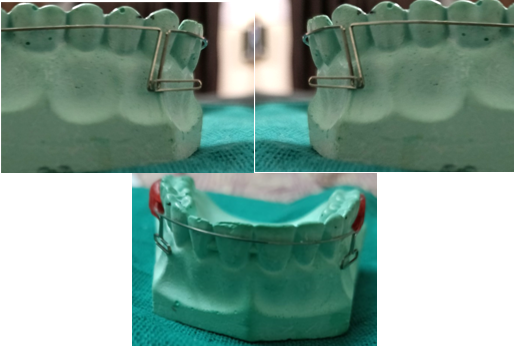
Opus loop-raymond E. siatkowski in 1977(Fig5)

In the study, closing loop design for usage in continuous arch wires was approached methodically. The moment-to-force ratio (M/F) equations are derived during the design phase using Castigliano's theorem in terms of loop geometry.2

The ascending legs are at an angle of 70 degrees to the plane of the brackets, and the apical horizontal leg is 10mm long. The ascending legs, especially the apical loop legs, must be spaced apart by no more than 1 mm. Opus loop has the ability to deliver M/F between 8.0 and 9.1 mm. Dimensions: 0.5 mm radius, 10 mm radius, and 10 mm height. It is made of 0.016 to 0.022 inch stainless steel wire, 0.018 to 0.025 inch stainless steel wire, or 0.017 to 0.025 inch TMA wire. Opus 90 and Opus 70 are two variations on the Opus loop.

Figure 4

Opus Loop

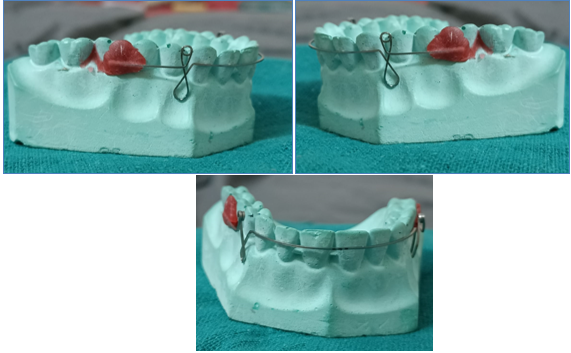
PG retraction spring- poul Gjessing in 1985 (Figure 6)

The final spring design was created using 0.016 x 0.022 inch stainless steel wire and was refined utilising a step-by-step process on a bench testing setup. The ovoid double helix loop that extends 10 mm apically is the main active component. Instead of correcting rotations and/or excessive deviations in inclination of the canine, the spring is designed to resist rotational and tipping tendencies during retraction. Therefore, it is required to stop levelling the buccal segments before inserting the spring. Pulling away from the molar tube until the two halves of the double helix are separated by 1 mm results in activation to 140 to 160 gms. This process is repeated every 4 weeks. After retraction, lingual elastics can be used to readily correct any minor canine rotations that may have occurred due to anatomical variations in the root structure.3

For the anterior section, the moment-to-force ratio is significant, ranging from 7 mm to 10.5 mm at 3 mm and 1 mm activation, respectively. These numbers aren't as high as what Gjessing stated.5

Figure 5

Pg Retraction Spring

Figure 6

Tear drop loop

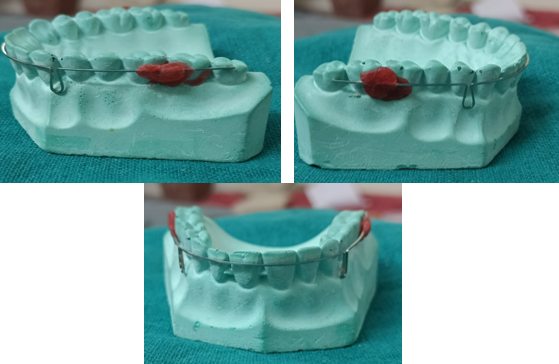
Tear drop loop - by R. G. alexander (Figure 7)

Mandibular incisor movement requires an optimal force of about 2.60 N to be delivered. The teardrop springs of 6 mm height activated by 0.5 mm, which gave 2.51 N force, and the teardrop loop of 8 mm height activated by 1.0 mm, which provided 2.77 N force, were the springs that came closest to this value. The values of the teardrop loops were less than 2.60 N for heights of 7 mm, less than 1.89 N for heights of 8 mm, and less than 1.37 N for heights of 0.5 mm when activated. The forces applied to the 7 and 8 mm high teardrop loops when they were activated by 1.5, 2.0, and 3.0 mm were greater than the optimal values for mandibular incisor movement.

Figure 7

Box Loop

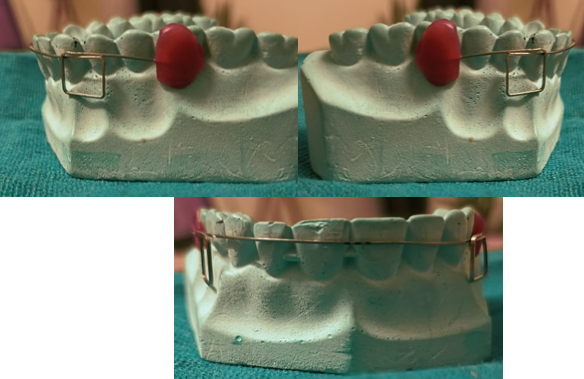
Box Loop - A. sivakumar in 2006 (Figure 8)

The clinician can assess the moment-to-force ratio applied to the active unit. The point of force application in reference to the horizontal dimension of the "box" determines the direction of moments created at the loop. Any force and moment ratio— force, pure moment, or any other combination—can be released at the anterior bracket by activating the rectangular loop. By selecting various force application sites, adjusting the horizontal dimension of the loop, or angling the horizontal branch of the loop in relation to the bracket of the active unit, it is possible to get the required combination of moments and forces. Low load deflection rate is present.

Figure 8

Omega Loop

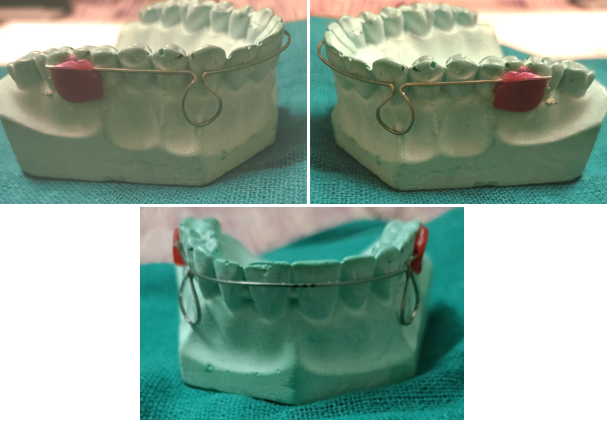
Omega Loop- Morris M. Stoner in 1960 (Figure 9)

Morris M. Stoner published a description of an alternative to the open vertical loop in 1960. Due to its likeness to the Greek letter omega, after which it is named, it was given that name. Its advantage over an open vertical loop is that it is less likely to fracture due to a more even stress distribution along the loop's curvature as opposed to a concentration at the apex. It is frequently employed as a molar stop and for the physical movement of the root.5 Gandhi et al. explained how to use a modified omega loop to close a maxillary midline diastema by inserting two crimpable hooks on the loop's arms that are orthogonal to one another. The closing force came from an E-chain stretched between the hooks provided the activating force to close the midline diastema.7, 8

Figure 9

Reverse Vertical Loop

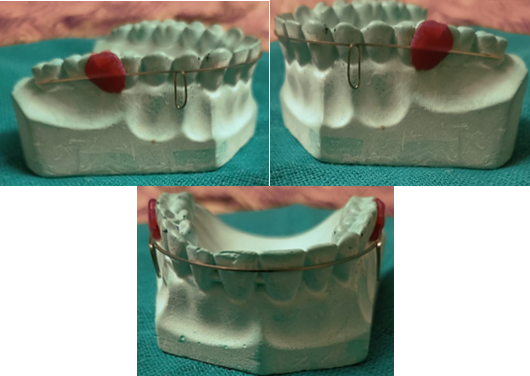
Reverse vertical loop- Dr. R. H. Strang in 1933 (Figure 10)

The Bauschinger effect states that a closed loop has a wider range of activation than an open loop. Its activation range is quite constrained, and it also produces an M/F ratio that is far from optimal if controlled tipping or translation is desired. These are its two main drawbacks. In Beggs mechanotherapy, archwires with vertical loops are used to align the anterior teeth. The loops make the wire spread wider between the teeth and result in softer pressure when the object is moved. A circular cuspid hook that lies on either side of the mesial aspect of the cuspid bracket is used to create the looped arch. In order to create overcorrection of rotations, labio-lingual movement, or mesio-distal movement, the loops are then activated.

Figure 10

Snail Loop

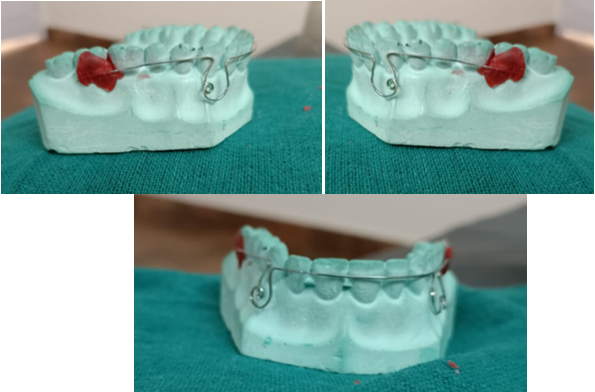
Snail loop -Dr. Pavan kumar vibhute in 2004 (Figure 11)

Snail loop is spiral shaped and designed for en masse space closure of the anterior teeth. The snail loop is fashioned from 0.017"x0.025" stainless steel wire by bending a simple omega loop into a spiral shape, which provides the forces and moments. The outer portion of the snail loop is 8mm high and 6mm wide and the inner portion is 6mm high and 3mm wide. The snail loop has the potential for twice as much activation as a stainless steel omega loop before undergoing permanent deformation. The outer portion of the snail loop is 8mm high and 6mm wide, and the inner portion is 6mm high and 3mm wide

Figure 11

Mushroom Loop

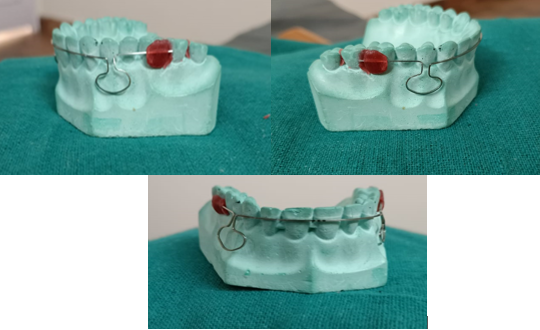
Mushroom Loop - Drs. Flavio uribe and eavindra nanda in 2003 (Figure 11)

The moment to force ratio produced by this looping arch-wire is optimal for translation. Additionally, the loop does not interfere with the gingival tissue and does not easily distort, which improves the delivery of the orthodontic load. 0.017" x 0.025" β-III At distances that have been standardised between 26 and 46 mm with a 2 mm increment, Connecticut new arch-wire is utilised. The distances between the lateral incisors' distal surfaces are measured in millimetres. Pre-activation of the 3mm leg separation and any necessary anchorage reinforcement are done anteriorly. Reactivation of the loop is delayed until a space closure of 3 mm, ensuring that the moment to force ratio remains constant.9